Vectorization Explained, Step by Step
Vectorization is one of the most useful techniques to make your machine learning code more efficient. In this post, you will learn everything you need to know to start using vectorization efficiently in your machine learning projects.
Share on:

Background image by Joel Filipe (link)
Outline
In this post, we will go over what vectorization really is, what the benefits of vectorizing your code are, and how you can do so. You do not need to have any specific knowledge prior to reading this post, but it will be very helpful if you are familiar with linear regression and the mean squared error since we will use those as an example. If you are not, I recommend you read the post Linear Regression Explained, Step by Step, where you will learn everything you need to know about those two. This post and the linear regression post, in particular, go hand in hand, as the examples in this post are taken directly from linear regression itself. We will also use the same dataset and terminology that was used in the post about linear regression, so even if you are familiar with linear regression, you might still find it helpful to just quickly skim through the linked post.
The main idea
If you’ve implemented a few machine learning algorithms on your own or if you perform many calculations in your programs, you know how long those calculations can sometimes take. Let’s say we have a dataset containing 100.000 data points and we want to perform some sort of operation on every single one of those points. If we use a regular loop for this, things will get very inefficient very quickly. If we can instead vectorize our operation and just perform one (or a few) large vector or matrix operation using something like NumPy, our code will run a lot faster
Vectorization
Example 1: Linear Function
Let’s say we want to use linear regression to predict the price of a house based on the number of bedrooms it has. We could create a linear function like this one:
where x is the number of bedrooms in a house. Ok. Now let’s say we want to predict the price of a house based on the number of bedrooms, the year it was built in and the average house price in the city the house stands in. Then our function would look more like this:
Things got less pretty rather quickly.. So to make our lives easier we will vectorize our initial equation! There are a couple of steps we need to take in order to vectorize our equation. First, we rename our and to and . So instead of writing
we now write
This will all make sense in a moment, just bear with me for now. Then we change up the notation of our function a little bit. We now write:
In this step, we rewrote our function to now use vectors instead of scalars. In other words, instead of multiplying a bunch of individual numbers together, we now only need to multiply two vectors. We define and like this:
where is our number of bedrooms for a given house. Let’s first check if this is equal to our initial definition.
If we calculate the dot product of our two vectors and , we get:
As we can see, our function remains unchanged!
But this might still look a bit confusing. Let’s go through the changes step by step.
We rewrote our and into the vector . So far so good. Next up we rewrite our input x into the vector . Ok, but what is this 1 doing in our ? Isn’t our x supposed to be the number of our bedrooms? Since we always want to add our bias term (now ) without multiplying it with anything (remember: our function looks like this: ), we need to account for that. By adding a 1 to our x-vector, we make sure that our bias-term is then multiplied by this 1, and therefor always added as is inside of our equation. This is also the reason why, in many books and tutorials, you will see people adding a 1 to their parameter vector. This is to account for the bias-term. Now you could write out the bias-term separately and just not add the 1 to your x-vector, but this way, our equation looks a bit neater on the surface. Both notations are used in practice, so now you know both sides of the coin! We also add this little to our to signal that we accounted for the bias-term already and to also differentiate this from any input we might also call “x”. So if you see an , remember that it means “x, but with a 1 added to account for the bias term”.
Example 2: MSE
So a non-vectorized definition of the MSE might look like this:
There is nothing wrong with that definition, but if we wanted to translate our definition into code, what we would probably do is create a loop that sums up each of the individual residuals. The code could look similar to this:
def mse_non_vectorized(data,function):sosr = 0 # sum of squared residualsfor (x,y) in data:residual = y - function(x)sosr += residual**2mse = sosr / len(data)return mse
Now, for our small dataset of 7 points that is no big deal, but imagine we had 100.000 data points (which is not uncommon today). Every time we wanted to compute our MSE, we would have to perform 100.000 operations through our loop. We can do better than this! So let’s vectorize our MSE!
For this, let’s use an exemplary dataset with two features: the number of bedrooms in a house and the price for that house. The dataset looks like this:
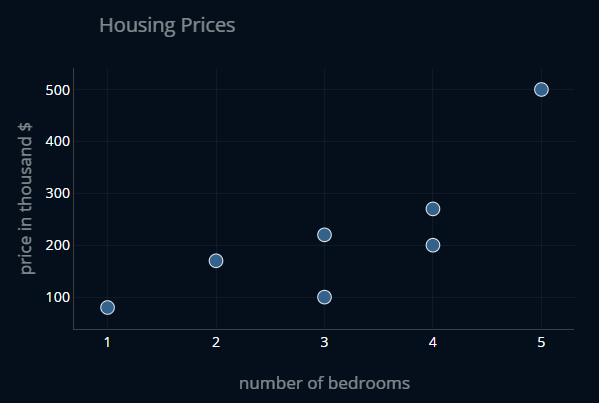
In Python, we can implement our dataset as a simple list:
data = [(1, 80), (2, 170), (3, 100), (3, 220), (4, 200), (4, 270), (5, 500)]
Let’s also create an exemplary linear function so we can calculate our MSE:
def f(x):return 60*x #number of bedrooms * 60k$ = price of the house
If we use our non-vectorized implementation of the MSE, we get:
>>>mse_non_vectorized(data,f)53400
Ok, now let’s vectorize it! First, let’s make some small changes. Let’s reshape our individual data values (1,80), (2,270) and so on into two vectors and . This will be useful later on when we redefine our MSE. Those vectors look like this:
With this, we can now redefine our MSE like this:
Remember, the part of the equation that is colored in blue is equivalent to . Ok, but what does this mean? Is this something like the “i-th power?” I’m glad that you ask! If we write out our equation in more detail once again, we get:
As we see, is the -th sample in our . Since we’ve already used the as a subscript, we just put the at the top, as a superscript. We write the in brackets to signal that this is not a power, but just an index-notation. I know this looks a bit off when you first see it, but at some point, you will get used to it. Note that we could have just not used as a subscript and put the at the bottom instead, but this way we do can show all of the necessary information, even though it looks a bit bloated.
And now, instead of taking the sum over every sample in our dataset, we instead calculate the error for every sample at once by replacing our sum with the following equation:
The part in blue is just the following:
Since this part represents the predicted prices of our function, we call it .
Now we can calculate the squares of residuals by taking the dot product of with itself:
This is okay to do since taking the dot product of a row vector with a column vector yields us a scalar. If we plug in the values for our concrete example and for our function , we get:
and if we take the dot product of this (transposed) vector with itself, we get:
which is in fact the same value that we got from our non-vectorized implementation of the MSE!
If we translate our new definition into code, we get:
def mse_vectorized(y, y_predicted):error = y-y_predicted # save y-y_pred in a variable so that we only have to compute it onceloss = 1/(y.size) * np.dot(error.T, error)return loss
We now no longer need to pass in our entire dataset as well as a function to our MSE.
Instead, we calculate beforehand, like this: y_predicted = f(x).
This makes our function a bit more lightweight.
Great, now we have vectorized our MSE as well!
Speed Comparison
Ok, now let’s test both of our implementations on an exemplary dataset. But for a real test, our small dataset is not going to cut it. Since our dataset does not really have to make sense, we can just use some random numbers. Let’s create an array with roughly one million values and reshape it to contain individual arrays [x,y]. Then we can also save x and y separately.
arranged_values = np.arange(1,100000,0.1).reshape(-1,2) #shape: (499995, 2)arranged_values.shapex = arranged_values[:,0]y = arranged_values[:,1]
If we now time the executions of our non-vectorized and our vectorized MSE using the magic command
%%timeit (you can learn more about those here),
we get this:

As you can see, the vectorized version outperformed the non-vectorized one by a landslide!
Further reading
If you are interested in applying vectorization to a linear regression problem, I highly recommend you read the post Linear Regression Explained, Step by Step, where you will learn everything you need to know about linear regression and use vectorization in practice.
Share on:
