How to Split Your Dataset the Right Way
If you are just starting out in machine learning and building your first real models, you will have to split your dataset into a train set as well as a test set. But what benefits does this splitting yield? How can you split your dataset optimally? In this article, we will go through these questions and explore why splitting your dataset makes sense and how you can split your dataset properly.
Share on:

Background image by Mario Gogh (link)
Outline
In this article, you will learn why you should split your dataset into a training and testing subset, how you can do so with just a single line of code and how this can increase the robustness of your machine learning model. Let’s begin!
Prerequisites
For this article, I’ll assume that you are familiar with at least one (supervised) machine learning model. It does not matter that much which one it is, but you should know at least one of them. If you don’t know a machine learning model, I’d recommend you read Linear Regression Explained, Step by Step and then come back to this article. In the linked article, you will learn everything you need to know about linear regression and implement it step by step in raw Python and with scikit-learn. Also, I highly recommend you read the article about bias and variance prior to reading this article, as it lays the groundwork for this post. By reading that article, you will learn everything you need to know about bias and variance, two fundamental concepts necessary to understand and compare machine learning models.
Training and Testing
Now, why do we even need to split our dataset? Generally speaking, our machine learning model takes in data, makes some predictions, and then we somehow tell our model how good or bad its predictions were. Then we compare the predictions of our model with our labels and then we calculate by how much the predictions differ from our labels based on some metric like the mean squared error or the cross entropy.
The more data we use to train our model, the more opportunities it has to learn from its mistakes, the more insights it can extract from the data it has been given, and the better the resulting model will be at predicting our labels
A Practical Example
Let’s say we have a dataset of exam scores where every entry in the dataset contains the number of hours a particular student spent studying for that exam as well as the number of points that student achieved in said exam. The dataset looks like this:
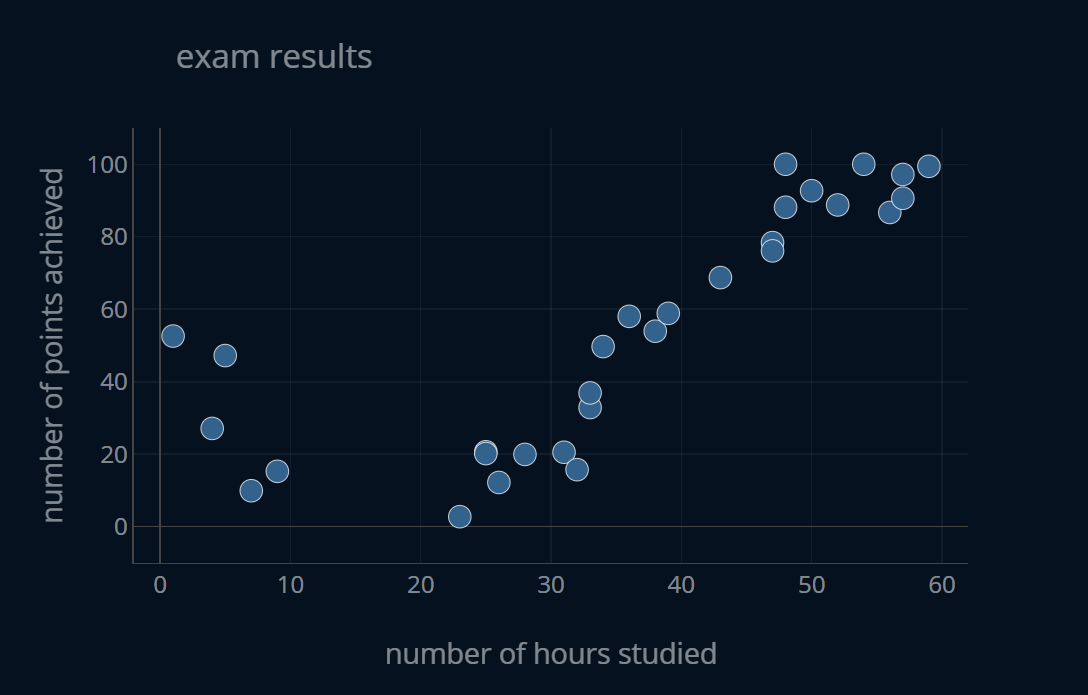
We now use polynomial regression
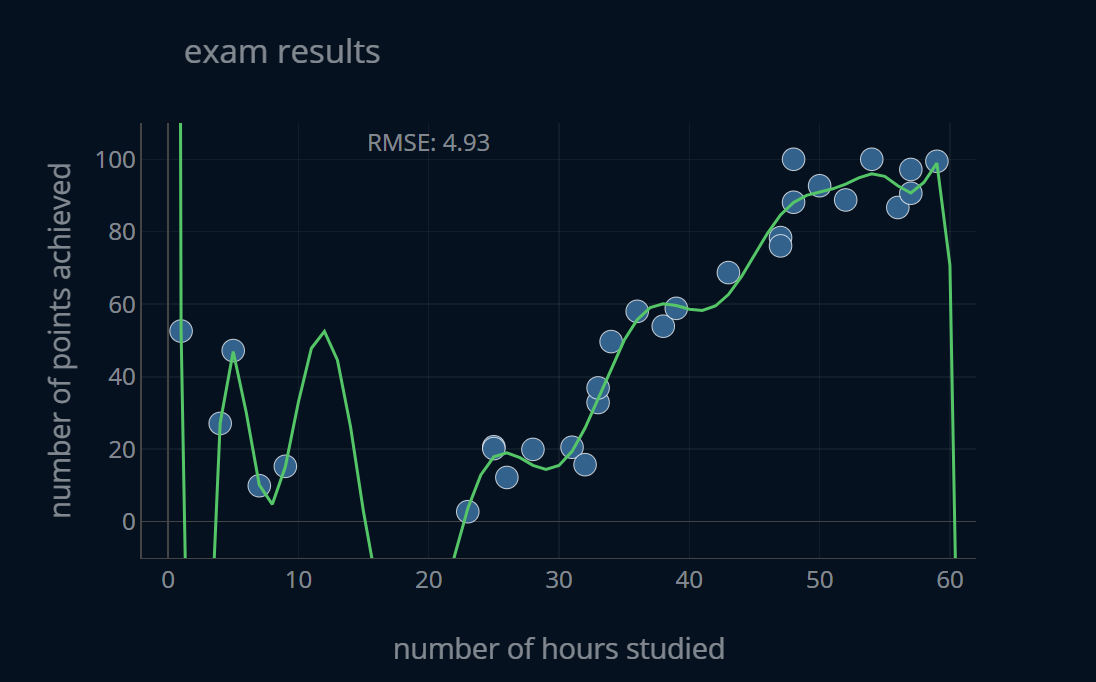
As you see, this model has a very low error (it has a root mean squared error, or RMSE, of about 4.93). In other terms, it has very low bias. However, this model also has a very high variance. After reading the article about bias and variance, we can say that this model is overfit.
This becomes even clearer when we split our dataset into a training portion and a testing portion. We still use our overfit model, but this time we train it only on the training data and then evaluate its performance both on the train set as well as the test set. This allows us to reason about the variance of this particular model. Take a look at the following plot:
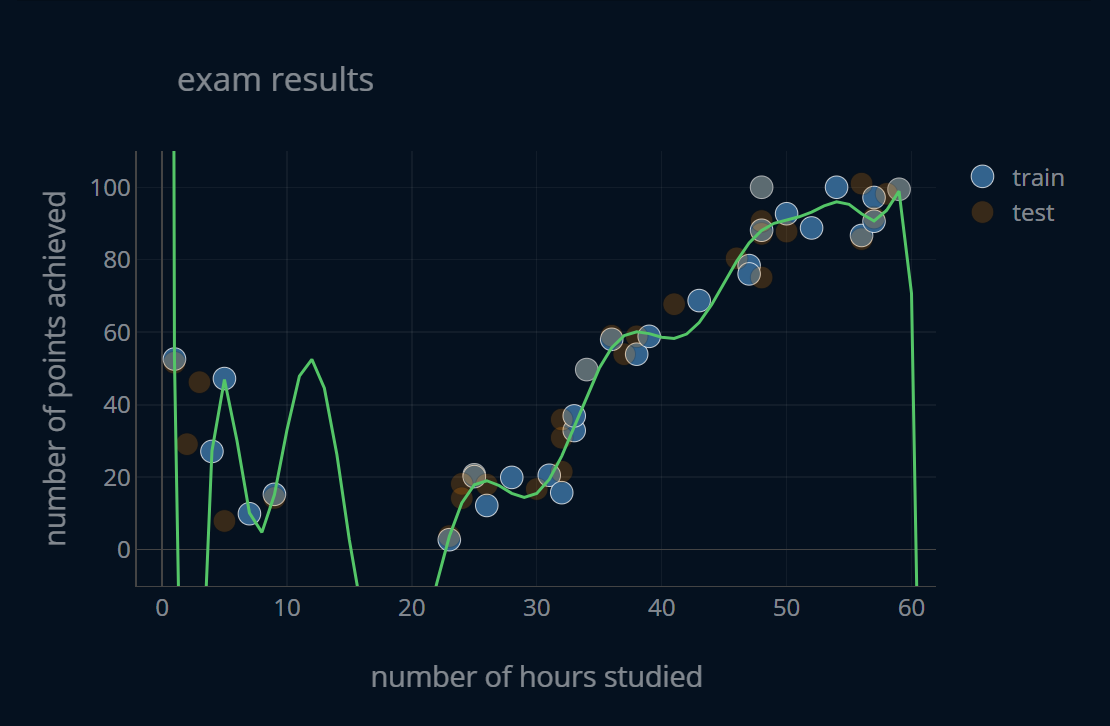
Above the plot, you can see the RMSE for the polynomial regression model with regard to the currently displayed dataset as well as the relative difference (R.DIFF) between the initial RMSE and the current RMSE. When you load the plot, R.DIFF will be equal to 0, since the current RMSE is also the initial RMSE. By pressing the button at the top, you can toggle between the train and test set. Once you switch to the test set, you will notice a pretty significant increase in the RMSE. To be more exact, you will see an increase of 17.16%. If you’ve read the article about bias and variance, you will recognize this as a key sign of overfitting.
We would have no way of diagnosing this overfitting if we did not have a dedicated test set. If we did not have a test set, we would only find out that our model is overfit once it was actually being used to predict new data! So by splitting our dataset into a train set and a test set, we can evaluate our model in a realistic scenario and prevent it from overfitting.
An Analogy
I really like analogies, and maybe you do to. If you do, then this might be a paragraph worth reading. If you don’t, feel free to skip ahead to the next section, Common Questions.
I like to think of a student preparing for their mathematics exam (or really, any other subject). The professor provides the student with exercise sheets and corresponding solutions which the student can use to prepare for the exam. However, when the student takes the exam, they are presented with the exact same exercises as the ones they were given on the exercise sheets. Of course, the student aces the exam because they have trained on exactly these questions. But the professor can’t actually tell whether the student really understood the material and learned to solve these problems efficiently, or whether they just memorized every single possible question and its corresponding answer without learning anything. This happens when the professor does not have a “test set” of exercises ready to evaluate the performance of their “model”, or in this case, their student. The professor needs to have some sort of “final exam” for the student so that they can test whether or not the student truly understood the material. The final exam needs to have questions similar to the ones in the practice material, but it also has to contain some questions the student has never seen before.
In our case, you are the professor, and your machine learning model is your student. You have to take care of your pool of exercises and make sure that you teach your student to truly understand the material, and not just to memorize all the answers.
Common Questions
When the train and test sets are first introduced in a machine learning class, there are usually a number of questions that arise, and some additional questions that arise after you first try to implement dataset splitting in your own machine learning projects. Here, I want to go over some of the most common questions asked.
How Large Should the Testing Set be?
I want to tell you the most important thing upfront: There is no clear answer to this question. This is because test set size is a hyperparameter which we have to determine ourselves before training our model.
The optimal value for the size of your testing set depends on the problem you are trying to solve, the model you are using, as well as the dataset itself.
If you have enough time on your hands, you could just try out a 60-40-split (that is, use 60% of your data for training, and 40% of it for testing), a 70-30-split, an 80-20-split, and so on. Then you could compare the test scores for each of these splits and take the split where the test error is the lowest. However, this can take a lot of time and computing power, and in most cases it won’t even make a huge difference in your testing error. So with that being said, what are some general rules we can follow to decide how large our test set should be?
Usually, you can estimate how much data you will need for testing based on the amount of data that you have available. If you have a dataset with anything between 1.000 and 50.000 samples, a good rule of thumb is to take 80% for training, and 20% for testing. The more data you have, the smaller your test set can be. If you have 1.000.000 samples, you would probably be fine by reserving just 1% for testing and using the remaining 99% for training. But when you have less data than that, things start to get more tricky. On one hand, you want to use as many samples as possible from your already small dataset to train your model. On the other hand, you also need to use a higher percentage of your data for testing to get a realistic performance estimate, exactly because your dataset is so small. The only thing in this scenario that is (almost) guaranteed to increase your model performance is to “just get more data”, as bluntly as it sounds. If applicable to the problem, you can also try to synthetically generate more data using something like Data Augmentation.
Which Part of the Dataset Should be Used For Testing?
If you have never split your dataset into a training and testing subset before, you might ask yourself which part of the dataset should be used for training and which part should be used for testing. Does it even matter? Well, maybe. If your dataset contains some sort of relevant order, then you should definitely use a specific portion of it. An example of this would be time series data, which is ordered according to time.
So if you are trying to jump on the Bitcoin-Hype and build a machine learning model to try and predict the future price of Bitcoin based on a dataset containing the price of Bitcoin for every week of the past 5 years, then it would not make a lot of sense to shuffle this dataset. This is because by shuffling your dataset, you are distorting the ordering of your data, which in this case, is something we want to keep. If your dataset does not follow any such intrinsic order, then you should definitely shuffle your dataset and take a random subset for training and testing. Why?
If you don’t shuffle your dataset and take say the first 20% of your dataset for testing, you might just be unlucky and get disproportionately many samples from one class/from one specific interval, because the data was not properly shuffled before. Maybe the person creating the dataset “partially sorted” the dataset unintendedly. Imagine you have a dataset of mathematics exam questions, containing linear algebra, calculus, and probability questions. The person who assembled the dataset might have written most of the linear algebra questions on one day, written the calculus questions on another day, and written the probability questions on a third day. Then they just combined all of these questions and formed a dataset. As a consequence, the first part of the dataset may contain disproportionately many linear algebra questions. Why is this bad for our model?
If we think back to our analogy with the student, imagine the student only gets linear algebra practice problems. But on the exam, they see a problem from calculus! This would not be a great situation for our student. Similarly, if our model is trained mostly on linear algebra questions, it will specialize in those types of questions, just like our student. Therefor it will not be as good at solving calculus questions. At the same time, our test set contains a lot more calculus questions than linear algebra ones, because we used most of the linear algebra questions for training. So not only is our model best at solving linear algebra questions, but our test set also contains fewer algebra questions than any other question category! This is a lose-lose situation.
What makes this worse is that this mistake can be extremely difficult to find.
If your model is underperforming, you will likely try out a more complex model,
look for outliers in the dataset, etc. But forgetting to shuffle your dataset before splitting it
is a very subtle mistake and finding it can cost you a lot of time and energy.
Fortunately, if you are using scikit-learn’s train-test-split-function (which we will take a look at in a second),
it will shuffle your dataset by default, so even if you forget to set shuffle=True, the function will still do
it for you. Nevertheless, it is important to remember that shuffling your dataset before splitting it is
something that can have a non-trivial effect on your model performance.
So in summary, if your data has an ordering, don’t destroy it, and if it does not have an ordering, make sure to shuffle the dataset before splitting.
What is Stratification?
In the previous question we saw how having disproportionately many samples of one kind in only the train set or only the test set is a very uncomfortable position to be in. Now, what if I told you that there is a way to make sure this never happens?
Let’s assume for a second that we are dealing with a classification-based task, meaning we have some features and a finite amount of discrete labels which we are trying to predict using the features. We’ll come back to regression in a moment. In the case of a classification problem, the distribution of labels should be roughly the same for both the training and the testing set.
So if we think of this in terms of our analogy, if the mathematics exam our student has to pass contains linear algebra questions, calculus questions, and probability questions, then the exercise sheets should roughly follow these relative amounts.
When we split our dataset in this particular way, meaning we make the training and testing set have as similar as possible label distributions, we say that we create a stratified split.
How does this work under the hood? I don’t want to dive into too much detail,
but let’s look at how we might implement stratification ourselves.
Let’s say we have a dataset consisting of X and of y.
X is just an array of length 10 (the contents of X are not important for our example) and y is [ 0, 0, 1, 1, 0, 1, 0, 0, 1, 1 ].
It’s not really important what this data represents, we’ll just use it as “dummy” data to better understand stratification.
To start off, we can count the number of samples for each class, and then calculate each class percentage with regard to the size of the dataset. In our example, we have 10 samples with 2 distinct labels 0 and 1, and each label appears 5 times. This means that the relative frequency of label 0 is 0.5 = 50%, and the same is true for label 1. Now, we can calculate the number of samples needed for each class in our subsets.
Let’s say we want a train set with a size of 80% of the original dataset and a test set with a size of the remaining 20%. Since we have 10 samples, our train set will contain 8 samples and our test set will contain 2 samples. We now get the amounts of samples per label by multiplying the frequency of that label in our dataset by the subset size. In other words, the number of samples with the label 0 in the train set is equal to the label frequency of label 0 (0.5) multiplied by the size of the train set (8). This gives us 4. Similarly, we will need 0.5*2 = 1 samples with label 0 in our test set. Since label 0 and label 1 appear the same number of times in the dataset, the number of samples for label 1 are the same as for label 0. Now we know how many samples per label each subset should have.
The last step is to just pick samples with the corresponding labels and pack them together into a train set and a test set. We can do so by extracting all samples from the dataset that have a specific label, and then pick from the extracted values either randomly or in order.
So if you now come across a phrase like ” to create a stratified split”, you will know exactly what it means. Using stratification in your splits can be extremely easy, and we’ll take a look at some practical examples in the next section. But what about regression?
Since we are predicting a continuous range of values in regression, we can’t “count” the labels in the same way as we did for classification. In general, this means that stratification is not so trivial for regression, and as far as I know, there is no one-liner to create a “stratified” split for regression. However, that does not mean it’s not possible to come up with some alternatives. I don’t want to go into too much detail in this article because the topic is worthy of its own discussion, but if you are interested in reading more about this, I recommend you take a look at this blog article by Scott C. Lowe, which presents a couple of ideas in more detail.
How can I Efficiently Split my Dataset with Code?
So how can you split your dataset without having to write unnecessarily large amounts of code? It’s actually quite easy. All it takes is one line of scikit-learn-code and you’re done. Let’s take a look:
from sklearn.model_selection import train_test_splitX_train, X_test, y_train, y_test = train_test_split(X,y, test_size=0.3, random_state=42, shuffle=True)
We first import the famous train_test_split-function from scikit-learn, which takes the following parameters:
(*arrays, test_size=None, train_size=None, random_state=None, shuffle=True, stratify=None)
You only need to provide an argument for either the train_size or the test_size, because the other one will be set to just 1-(the size you provided).
If you provide a value for random_state, and execute this line of code multiple times, it will
always split the dataset in the same way. If you do not provide a value for random_state, the split will be different every time.
If shuffle is true, then the dataset is shuffled before it is split.
And lastly, we have stratify. Here, you can provide the subset which should be used to command the stratification of the dataset.
Let’s look at two quick examples.
Practical Example: Regression
Let’s consider the aforementioned dataset of exam scores. We have two arrays, namely X and y. X contains the number of hours every student studied, and y contains the number of points each student achieved on the exam.
Now we want to split this dataset into a train set containing 80% of the original data and a test set containing 20% of the original data. We also want to make the splitting reproducible. We can do this with the following line of code:
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size=0.2, random_state=42, shuffle=True)
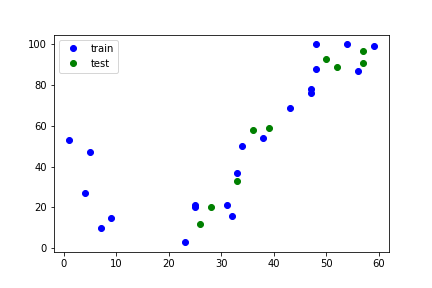
And that’s it! It really is that easy. If we want to, we can inspect our new train-and test-set with a simple matplotlib-plot:
plt.plot(X_train,y_train,".b",label="train",markersize=12) # ".b" means plot individual markers (".") in blue ("b")plt.plot(X_test,y_test,".g",label="test",markersize=12) # ".g" means plot individual markers (".") in green ("g")plt.legend()plt.show()
This yields the following plot:
Now let’s take a look at a classification-based example.
Practical Example: Classification
Now let’s say we have another dataset, describing exam tasks. The dataset has two features as well as one label value. Each main-task is described by 1) the number of sub-tasks the main-task has and 2) the number of characters the main-task has. So you can imagine that there is a main-task 1 with subtasks 1a, 1b, and so on (or 1.1, 1.2, etc.). Each task (main + subtasks) is then categorized into three levels of difficulty, namely easy, medium, and hard.
The dataset looks like this:
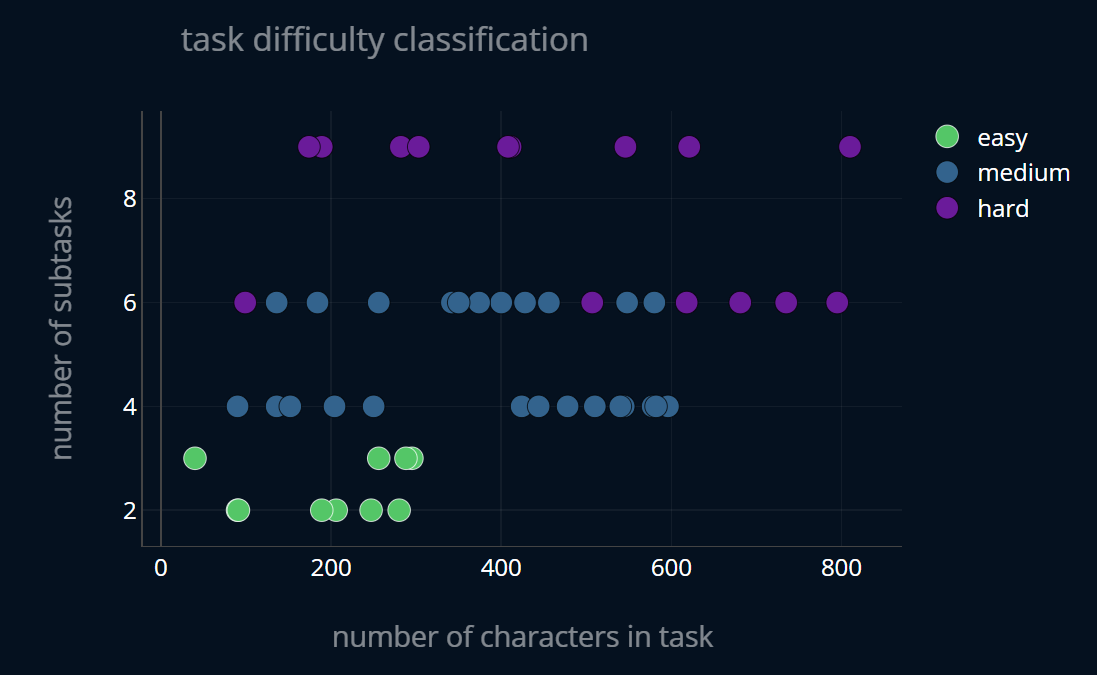
Now we want to split this dataset into a train set containing 70% of the original data, and a test set containing the remaining 30% and make the splitting reproducible. We can do this with the following line of code:
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size=0.3, random_state=42, shuffle=True)
If we also want to stratify our split with regard to our labels, we can do so by passing in y as the value
for the argument stratify, like so:
X_train_s, X_test_s, y_train_s, y_test_s = train_test_split(X,y, test_size=0.3, random_state=42, shuffle=True, stratify=y)
To make sure our stratification went as planned, we can use a few lines of matplotlib-code to display the label histograms of both our train set as well as our test set in the case where we did provide an argument for stratification, and in the one we did not. Let’s create the plot:
fig,ax=plt.subplots(1,2,figsize=(10,5))ax[0].hist([y_train_s,y_test_s],label=["train","test"],stacked=False)ax[0].set_xlabel("label")ax[0].set_ylabel("num samples")ax[0].set_title("stratified")ax[0].legend()ax[1].hist([y_train,y_test],label=["train","test"],stacked=False)ax[1].set_xlabel("label")ax[1].set_ylabel("num samples")ax[1].set_title("not stratified")ax[1].legend()
This yields the following image:
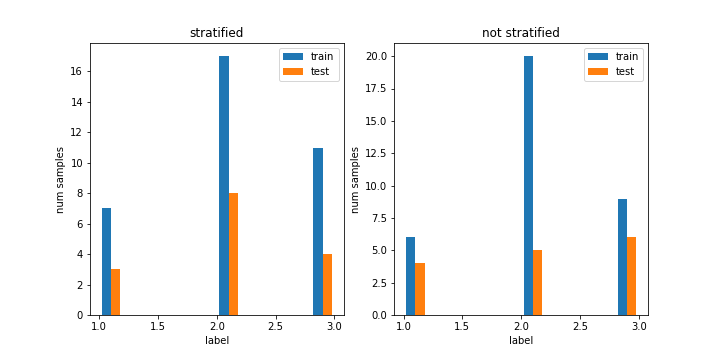
A Mistake?
The above plot does look a bit strange.. the histograms of the train set and the test set don’t seem to have similar column heights. Did our stratification fail? No, not at all! The issue here is that our histplot shows us the absolute amounts for each label. This means that it shows us the number of samples with label=1, label=2, label=3 there are in both sets. But in that case, if our test set is smaller than our train set, the amounts of samples for any label will probably be larger in our train set. So how can we overcome this? We can add weights to the histplot to get the relative values. Normally, each sample in a set is weighted with 1, which seems logical. But if we instead weigh every sample in the set with , then the sum of all weighted samples from one dataset will be exactly 1. This way we can display the relative class percentages instead of the absolute class amounts in our histplot. The adjusted code looks like this:
weights = [np.ones_like(y_train_s) / y_train_s.size, # np.ones_like generates an array of onesnp.ones_like(y_test_s) / y_test_s.size] # with the shape of the passed arrayfig,ax=plt.subplots(1,2,figsize=(10,5))ax[0].hist([y_train_s,y_test_s],label=["train","test"],stacked=False, weights=weights)ax[0].set_xlabel("label")ax[0].set_ylabel("num samples")ax[0].set_title("stratified")ax[0].legend()ax[1].hist([y_train,y_test],label=["train","test"],stacked=False, weights=weights)ax[1].set_xlabel("label")ax[1].set_ylabel("num samples")ax[1].set_title("not stratified")ax[1].legend()
which yields the following plot:
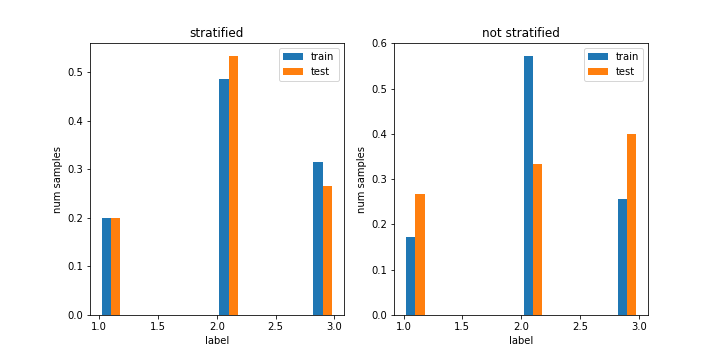
Here, we can clearly see the difference between the stratified split and the non-stratified (random) split. Nice!
“Breaking” Stratification
You may have noticed in the above image that even though our stratification worked correctly, the label amounts weren’t exactly equal in the train and test sets. They were off by just a little bit. Let’s look at a smaller example to understand why this is the case. If you have a dataset like this one:
X = np.arange(10) # = array containing the values 1..9, but X is not so important for this exampley = [1, 0, 0, 0, 0, 0, 0, 0, 0, 1] # 9 zeros and 1 one
and you want to split this dataset with an 80-20-ratio using stratification, like so:
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size=0.2, random_state=42, shuffle=True, stratify=y)
then you might end up with the following sets:
>>> y_train[0, 1, 0, 0, 0, 1, 0, 0]>>> y_test[0, 0]
Notice how the test set does not contain a single label of 1! This is because the relative amount of ones in our entire dataset is = 20%. Our test set contains two entries. 20% of 2 is equal to . Because we can’t have of a sample with label 1 in our test set, our splitting function just decided to not take in any sample with that label at all.
So in this example, stratification did not improve the quality of our split that much. So what can you do when you are in a situation like this? You have two options. Recall that, in stratified sampling, the number of samples with a particular label in a subset can be calculated as the product of the label frequency and the subset size. Right now our number of samples is , which is too low. We can increase that number by either 1. increasing the label frequency or 2. increasing the subset size. The first option is a lot more difficult than the second one because it likely involves getting more samples with that particular label, which is not always possible/affordable. Let’s see how both variants perform in practice.
- If we manage to get one more label of 1 into the dataset, like this:
X = np.arange(11) # now we have eleven values in our datasety = [1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1]
and again perform our 80-20-split, we will get something like this:
>>> X_train, X_test, y_train, y_test = train_test_split(X,y, test_size=0.2, random_state=42, shuffle=True, stratify=y)>>> y_train[1, 0, 0, 0, 0, 0, 0, 1]>>> y_test[0, 0, 1]
As we see, our y_test now contains a sample with label 1.
We can also increase the size of our test set from 0.2 to f.e. 0.3:
>>> X_train, X_test, y_train, y_test = train_test_split(X,y, test_size=0.3, random_state=42, shuffle=True, stratify=y)>>> y_train[0, 1, 0, 0, 0, 0, 0]>>> y_test[0, 0, 1]
which also adds a sample with label 1 to our y_test.
This problem should only be troublesome in cases where your data is particularly sparse (like the one shown here). But if you ever come across an issue like this, you’ll now know what to do in order to combat it.
Credit where credit is due, I have found this particular example on stackoverflow and found it so useful that I decided to include it in this article and extend it with a couple of code snippets and additional examples.
If you want to play around with this classification dataset on your own,
you can copy the code from this article and run it on your local machine.
Because we provided an argument for random_state, you should get the same results when you run the code
on your own machine!
Below you can find a drop-down containing the dataset as a code snippet.
Further Reading
If you have read a few tutorials on machine learning you might have come across a so-called validation set, or val set for short (sometimes it’s also called a development set, or dev set). If you have trained lots of machine learning models in the past, using a validation set might seem like second nature to you. But maybe, like I did when I first got into machine learning, you are scratching your head and asking yourself why a validation set is needed if we already have a test set. Which problem does the validation set solve? This question is so common and understanding why we need a val set is so important, that I want to dedicate an entire post to explaining what a validation set is, what problems it solves, and how you can start using validation sets in your next machine learning projects. Often times, truly understanding why validation is necessary can be something that differentiates someone who has a good understanding of how machine learning models are trained from someone who just knows how to write the code needed to train them. If you’re interested in reading more about this important aspect of training machine learning models, then I highly recommend that you read the article Why do We Need a Validation Set?.
Now, the validation set is one thing. But maybe you’ve also heard about cross validation. Maybe you’ve heard that it is a good practice in machine learning and that it also has something to do with a validation set. But maybe you are unsure as to how it really works or how you can integrate it in your machine learning projects. If this is you, then fear no more! After reading the article Cross Validation Explained, Step by Step you will understand exactly what cross validation is and how you can use it in your next machine learning project by adding just a few lines of code.
Share on:
